CoDEx Parafernalia
CoDEx is a package which can be used to calculate Wilson Coefficients (both tree level and one loop) for a given BSM theory in which heavy degrees of freedom with spin 0, 1/2 or 1. The Wilson Coefficients will be evaluated at the scale of the mass of the heavy particle.
 Functions available to the User
Functions available to the User Functions available to the User
Functions available to the User
There are some key functions, which let the user to define a list of BSM particles (along with their properties), build a Lagrangian, calculate the effective Wilson Coefficients
Help Function
re — re[expression] gives only the real part of expression.
im — im[expression] gives only the imaginary part of expression.
abs — Provides the norm of a vector. abs[A]= Sqrt[A.dag[A]]
hermitianConjugate — hermitianConjugate[a]=ComplexExpand[Conjugate[a]]
dag — Stands for the Dagger operation on some expression. That expression must be a list with more than one element. Otherwise, use hermitianConjugate.
commutator — commutator[a,b]=a.b - b.a (a and b should be matrices)
antiCommutator — anticommutator[a,b]=a.b + b.a (a and b should be matrices)
pau — Slightly modified version of PauliMatrix. pau[4]=*PauliMatrix[4]. Otherwise pau[i] = PauliMatrix[i].
del — del is a variation of a partial derivative operator. In del[a,expression], a is the Lorentz index, and runs from 0 to 3.
 Standard Model (SM) Fields
Standard Model (SM) Fields Standard Model (SM) Fields
Standard Model (SM) Fields
While writing the Beyond Standard Model (BSM) Lagrangian, the following SM fields have to be used.
In this CoDEx version, we consider only one generation Standard Model fields.
Fermion sector:
eLb1[i] , nuLb1[i] and eRb1[i] are the Lorentz conjugates ( ![]()
So, Quark Doublet, qdub[1,1] →![]()
uLb1[1,i] , dLb1[1,i], uRb1[1,i] and dRb1[1,i] are the Lorentz conjugates ( ![]()
Bosonic sector:
The SM bosonic sector consists of the SM Higgs doublet, three SU(2)L gauge bosons and eight SU(3)C gauge bosons (gluons).
A — SM Isospin gauge bosons. Acts like a vector with three components. Each component behaves like a spin 1 field.
bYvec — SM abelian gauge boson. Acts like a spin 0 field.
gluons — SM color gauge bosons. Acts like a vector with eight components. Each component behaves like a spin 1 field.
Field Strength
 Operator Bases
Operator Bases Operator Bases
Operator Bases
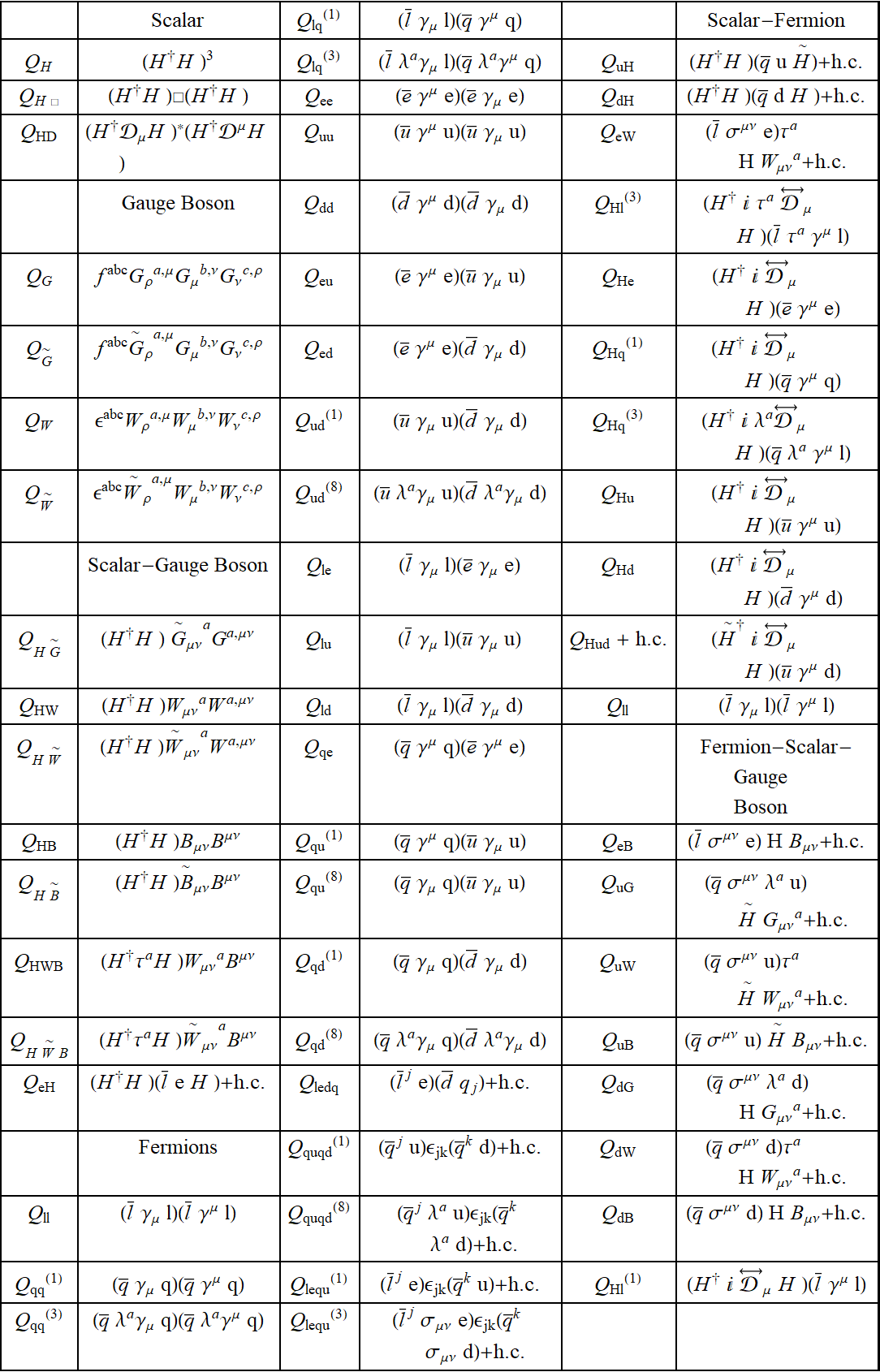
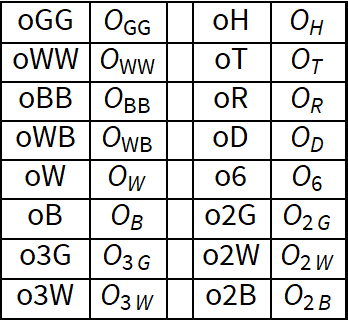
CoDEx can find Wilson coefficients according two bases of SMEFT operators, namely "Warsaw" and "SILH". They are listed below. Their details can be obtained in this page. Below are the operators in a grid format.
Warsaw Basis
|
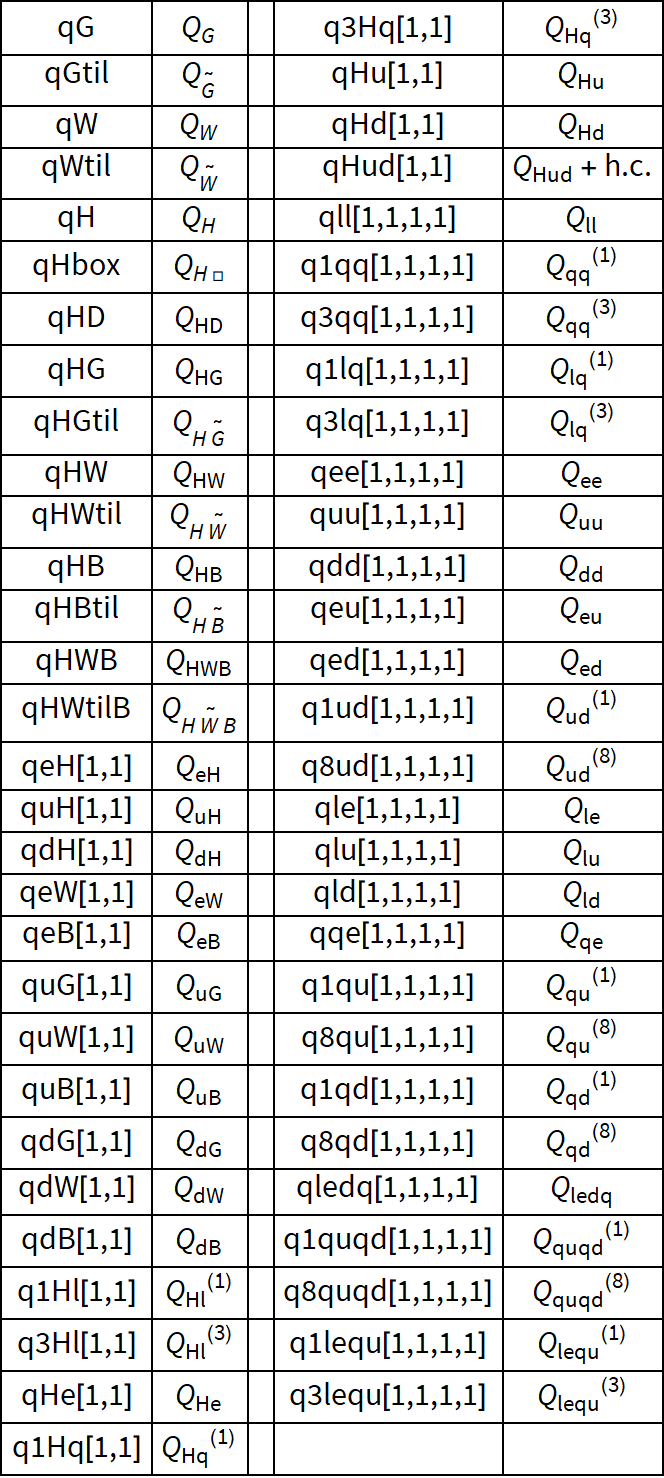
These operators are represented in the code as:
|
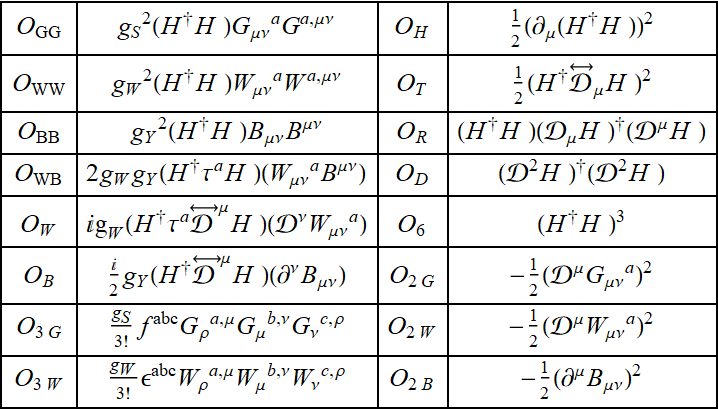
SILH Basis
|
These operators are represented in the code as:
|